Dynamic programming to check interleaving strings

 Given strings A, B and C, this approach finds whether C is formed by the interleaving of strings A and B.

Let us assume, A = "ab", B="cd" and C="acbd", then we can say that C is formed by interleaving of strings A and B.

But if  A = "ab", B="cd" and C="adbc", then we can say that C cannot be formed by interleaving of strings A and B. This is due to the fact that in C, the character 'd' has come before C.

if  A = "ab", B="cd" and C="abcdx", then also we can say that C cannot be formed by interleaving of strings A and B. This is due to the fact that in C has a character which is not in A or B.

Now, let us assume C is a 50 character string and A is a 20 character string and B is 30 character string. If C can be formed by interleaving of A and B, then any prefix of C can be formed by interleaving some prefix of A and some prefix of B.

Assume A(n), B(n), C(n) denotes the prefix of A with n characters, prefix of B with first n characters and prefix of C with first n characters. 

Assume C(20) can be formed by interleaving of some prefix of A and B. We know that C(20) can be formed by some combining characters of A(0),B(20) or A(1), B(19) or A(2),B(18),.................., A(18), B(2) or A(19), B(1) or A(20),B(0) etc. There can be 21 such combinations and characters interleaved from some of these combinations result in C(20).

Now let us check if C(21) can be formed by interleaving some prefixes of A or B. It will be possible if A(i),B(j) gives C(20)  (i.e. i + j == 20) and either A[i+1] is same as the 21st character of C, or B[j+1] is the 21st character of C. Assume A[i+1] is same as  21st character of C, then we can say that A(i+1),B(j) can be interleaved to form C(21). 

In dynamic programming, we use the stored results previously computed. For checking C(21), we check for all combinations of A(i),B(j) where i + j = 20 and 0 <= i,j <= 20 and all combinations are already computed. 

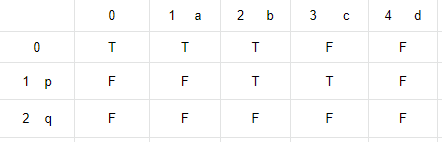
Now let us look at the below example. We will see how we check if C="abpcqd" is interleaving of A="abcd" and B="pq".

We initialize a two dimensional matrix of M size (2+1)x(4+1) and set all the cells to false. If M[i][j] is true, then first 'i' chars of B and first 'j' chars from A can be interleaved to get the string with first 'i + j' chars from C.

We have taken a matrix of 3x5 dimension.  Row 0 finds how much of C can be formed by interleaving only chars from A, and taking 0 chars from B.  M[0][0] = T (true) as null string from C can be formed by taking 0 chars from A and B.  

Now let us fill all the values for Row.  Row[0][1] = T, because  C(1) can be formed by A(1) alone.

Row[0][2] will be T again, as C(2) can be formed by A(2) alone. Row[0][3], Row[0,4] remain F as C(3) and hence C(4) also cannot be formed from A(3) and A(4) alone. 

Row[1][0] will remain false as C(1) cannot be formed from B(1) alone. Similarly Row[2][0] remains false.

  

Now let us start modifying Row[1] values. M[1][1] will remain F. Because though M[0][1] is T, C[1+1 - 0] = C[1] != B[0].  Row[1][2] will be T, as M[0][2] is true (that means C(3) is containing 'ab') and C[1+2 - 1]=C[2]==B[1].  Row[1][2] = T means, C(3) can be formed by interleaving B(1) and A(2). Now Row[1] is only for taking 1 char B[0] from B. As Row[1][2] is T, so for subsequent comparison on this row, we will use chars from A only. Row[1][3] will be T as Row[1][2] is T and C[3] == A[2]. Row[1][4] will remain F, as though Row[1][3] = True,  but C[4]!=A[3]

Similarly, we check Row[2]. Row[2][3] will be T as Row[1][3] == T and C[4] == B[2]. 

Row[2,4] will be T as Row[2][3] == T and C[5] == A[3].

Python implementation of above algorithm is given below:

'''
Given A, B, C, find whether C is formed by the interleaving of A and B.

Example:
1:
  A = "ab"
  B = "cd"
  C = "acdb"
  Here, C can be formed by the interleaving of A and B

2:
  A = "ab"
  B = "cd"
  C = "adbc"
  Here, C cannot be formed by the interleaving of A and B
  as 'd' and 'c' are coming out of orders in C.

2:
  A = "ab"
  B = "cd"
  C = "acd"
  Here, C cannot be formed by the interleaving of A and B
  as 'b' is missing in C

'''

def is_interleaving(first, second, interleaved):
    if len(first) + len(second) != len(interleaved):
        return False;
    if len(first) == 0:
        return second == interleaved
    if len(second) == 0:
        return first == interleaved

    # interleaved must start with 0th char of first or second string
    if not first[0] == interleaved[0]  and not second[0] == interleaved[0]:
        return False


    i = len(first) + 1
    j = len(second) + 1

    k = 0
    matrix = []
    while k < j:
        matrix.append([False] * i)
        k += 1

    # 0 char from first, 0 char from second is equal 0
    # char from interleaved
    matrix[0][0] = True


    # Now check how much of interleaved string can be formed 
    # by using 0 char from second and all others from first

    k = 1
    while k < i:
        if matrix[0][k - 1] and  (first[k - 1] == interleaved[k - 1]):
            matrix[0][k] = True
        else:
            break
        k += 1
    
    # Now check how much of interleaved string can be formed 
    # by using 0 char from first and all others from second

    k = 1
    while k < j:
        if matrix[0][0] and  (second[k - 1] == interleaved[k - 1]):
            matrix[k][0] = True
        else:
            break
        k += 1

    # Now we successively find out if interleaved[:n+m] can be formed
    # by interleaving first n chars from first and m chars from second
    # m varies from 1 to len(first)
    # n varies from 1 to len(second)
    # When we are on xth row of the matrix, we are actually trying to
    # check if (x - 1) chars from second string have been already seen,
    # and for that to happen, x - 2 chars have to be already present
    # in some prefix of interleaved. 

    k = 1
    ksecond_matched = False
    while k < j:
        #checking for a prefix of interleaved which can be formed
        #with k chars from second 
        l = 1
        ksecond_matched = matrix[k][0]
        while l < i:
            if not ksecond_matched:
                if matrix[k-1][l] and interleaved[k + l - 1] == second[k-1]:
                    matrix[k][l] = True
                    ksecond_matched = True
            else:
                # we have already matched k chars from second, check if a prefix
                # of length k + x can be obtained which is interleaved with
                # first k and x chars from second and first respectively
                if matrix[k][l - 1] and interleaved[k + l - 1] == first[l-1]:
                    matrix[k][l] = True
            l += 1
        k += 1
    
    return matrix[j - 1][i - 1]



test_data = [['a', 'b', 'ab', True],
             ['ab', '', 'ab', True],
             ['abc', 'd', 'abcd', True],
             ['ab', 'cd', 'abcd', True],
             ['ab', 'cd', 'abcde', False],
             ['ab', 'cde', 'aced', False],
             ['ab', 'cde', 'abcd' , False],
             ['ab', 'cde', 'aecdb', False],
             ['ab', 'cde', 'abcde', True]]


for row in test_data:
    if is_interleaving(row[0], row[1], row[2]) != row[3]:
        print '!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!Failed for ', row
    else:
        print 'Passed for', row

C++ implementation of above algorithm is given below:

#include <string>
#include <iostream>
#include <vector>
#include <algorithm>
#include <tuple>

using std::string;
using std::vector;
using std::cout;
using std::endl;
using std::tuple;
using std::make_tuple;
using std::get;


bool is_interleaving(const string& first, const string& second, 
    const string& interleaved)
{
    if (first.size() + second.size() != interleaved.size()) {
        return false;
    }
    if (first.size() == 0) {
        return second == interleaved;

    }
    if (second.size() == 0) {
        return first == interleaved;
    }
    
    if (second[0] != interleaved[0] && first[0] != interleaved[0]) {
        return false;
    }

    int i = first.size() + 1;
    int j = second.size() + 1;

    int k = 0;
    vector<vector<bool> > matrix;
    while (k++ < j) {
        matrix.push_back(vector<bool>(false,i));
    }

    // 0 char from first, 0 char from second is equal 0
    // char from interleaved
    matrix[0][0] = true;

    // Now check how much of interleaved string can be formed 
    // by using 0 char from second and all others from first

    k = 1;
    while (k < i) {
        if (matrix[0][k - 1] &&  (first[k - 1] == interleaved[k - 1]))
            matrix[0][k] = true;
        else
            break;
        k++;
    }
    
    // Now check how much of interleaved string can be formed 
    // by using 0 char from first and all others from second

    k = 1; 
    while (k < j) {
        if (matrix[0][0] &&  (second[k - 1] == interleaved[k - 1]))
            matrix[k][0] = true;
        else
            break;
        k++;
    }

    // Now we successively find out if interleaved[:n+m] can be formed
    // by interleaving first n chars from first and m chars from second
    // m varies from 1 to len(first)
    // n varies from 1 to len(second)
    // When we are on xth row of the matrix, we are actually trying to
    // check if (x - 1) chars from second string have been already seen,
    // and for that to happen, x - 2 chars have to be already present
    // in some prefix of interleaved. 

    k = 1;
    int l = 0;
    bool ksecond_matched = false;
    while (k < j) {
        //checking for a prefix of interleaved which can be formed
        //with k chars from second 
        l = 1;
        ksecond_matched = matrix[k][0];
        while (l < i) {
            if (!ksecond_matched) {
                if (matrix[k-1][l] && interleaved[k + l - 1] == second[k-1]) {
                    matrix[k][l] = true;
                    ksecond_matched = true;
                }
            } else {  
                // we have already matched k chars from second, check if a prefix
                // of length k + x can be obtained which is interleaved with
                // first k and x chars from second and first respectively
                if (matrix[k][l - 1] && interleaved[k + l - 1] == first[l-1])
                    matrix[k][l] = true;
            }
            l++;
        }
        k++;
    }
    return matrix[j - 1][i - 1];

}


// test run

int main() {
    cout << "Running some tests for the implementation" << endl;
    vector<tuple<string, string, string, bool> > inputs;
    inputs.push_back(make_tuple("a", "b", "ab", true));
    inputs.push_back(make_tuple("ab", "", "ab", true));
    inputs.push_back(make_tuple("abc", "d", "abcd", true));
    inputs.push_back(make_tuple("abc", "d", "acbd", false));
    inputs.push_back(make_tuple("a", "bc", "ab", false));
    inputs.push_back(make_tuple("ab", "bc", "abbc", true));
    inputs.push_back(make_tuple("ab", "bc", "acbb", false));
    inputs.push_back(make_tuple("ac", "bc", "abbc", false));

    for_each(inputs.begin(), inputs.end(), [](tuple<string, string, string, bool>& data) {
            cout << "Cheking for str1 = " << get<0>(data) << "  str2 = " << get<1>(data) 
                << "    interleaved = " << get<2>(data) 
                << "  expected=" << std::boolalpha << get<3>(data); 
            if (is_interleaving(get<0>(data), get<1>(data), get<2>(data)) != get<3>(data)){
                cout << " --> Failed " << endl;
            } else {
                cout << " --> Success " << endl;
            }
    });    
}

Extending Redis with new operations to expire data

Recently, one of my juniors was working on something which needed a distributed cache for sharing states across multiple process and saving states across restarts. Also, we needed the support for setting an expiry as we wanted to get the keys deleted on its own. We started with using MULTI command of Redis along with multiple SET command with expiry values. It turned out that, every command is sent to Redis separately for MULTI transactions and that was not a good choice for us. Also MSET command only allows to set values for the keys and not allow to set the expiry for the keys. So, MSET also we could not use.

We switched to Redis pipelining and that looks fine. But one small problem I noticed was that, for a pipleline with batch of 1000 SET operations, I get a response buffer containing the replies for all the 1000 operations. That was not a very good option for me. I wanted to have just one overall response just like we get in case of MSET or MSETNX commands.

I looked around and found that Redis server side scripting with Lua is a great option here and it can pretty much do the needful. Below code sample for doing the work:

local keycount = #KEYS
local argvcount = #ARGV
if ((keycount * 2) ~= argvcount )
then
    return 0
else
    local valstart  = 1
    for i = 1, #KEYS do
        redis.call('set', KEYS[i], ARGV[valstart], 'ex', ARGV[valstart + 1])
        valstart = valstart + 2
    end
    return 1
end

The code will take and execute a series of "set key value ex expiry_in_second" command internally and will return 1 on SUCCESS and 0 on failure.

We will use the redis EVALSHA command to create a custom command on Redis. I put the code snippet in a file named redis_call.lua and used SCRIPT LOAD command to load the script to Redis:

$ redis-cli -h localhost -p 6379  script load "$(cat redis_call.lua)"
"24d044a0dcc3af12f1b418d828083c475df48e8f"

So, I can use the SHA1 digest "24d044a0dcc3af12f1b418d828083c475df48e8f" to set value and expiry for multiple keys. Check the below output from redis-cli.

$ redis-cli -h localhost -p 6379
localhost:6379> EVALSHA 24d044a0dcc3af12f1b418d828083c475df48e8f 2  key1 key2 value1 1000 value2 20000
(integer) 1
localhost:6379> get key1 
"value1"
localhost:6379> get key2
"value2"
localhost:6379> ttl key1
(integer) 985
localhost:6379> ttl key2
(integer) 19981

So the script worked and here we got a custom command that simulates MSET with expiry for each key.

But still I felt that if we can get some built-in commands like MSETEX which is "MSET with expiry for each key" and MSETNXEX which is "MSETNX with expiry for each key", things would have been much better.
It is pretty simple in Redis to add a new command. So, I cloned Redis github repo, and added code for MSETEX and MSETNXEX. The help for the commands describe what they do:

$ redis-cli -h 127.0.0.1 -p 6379
127.0.0.1:6379> help msetex

  MSETEX [m/s] key value expiryseconds_or_milliseconds [key value expiryseconds_or_milliseconds]
  summary: Set multiple keys to multiple values with expiry set to seconds or millisconds. 
  since: 6.0.0
  group: string

127.0.0.1:6379> help msetnxex
  MSETNXEX [m/s] key value expiryseconds_or_milliseconds [key value expiryseconds_or_milliseconds]
  summary: Set multiple keys to multiple values with expiry set to seconds or millisconds, if none of the key exists
  since: 6.0.0
  group: string

127.0.0.1:6379> 

So, I can use MSETEX to SET values to multiple keys and also their expiry times. MSETNXEX only if none of the keys exists.  Below are some example of their uses:

127.0.0.1:6379> MSETEX m keya valuea 100000 keyb valueb 200000
OK
127.0.0.1:6379> MSETNXEX m keya valuea 10 keyc valueb 200000
(integer) 0
127.0.0.1:6379> MSETNXEX m keyd valued 9999 keyc valuec 20000
(integer) 1

My code for adding the 2 new commands can be accessed here . I have raised pull request. Hopefully, the PR will be accepted.