Getting number of trees in a XGBoost model

 We can dump the number of trees in the xgboost model by below method:

Load the model and save it as a JSON file. Of course this step is not needed if the model was saved as a JSON already.

Then simply extract the num_trees information from the JSON file.

Below code snippet we may use for the same:

1. import sys
2. import json
3. import xgboost as xgb
5. if len(sys.argv) < 2:
6. print(f'Usage: {sys.argv[0]} ')
7. exit(1)
9. loaded_model = xgb.Booster()
10. loaded_model.load_model(sys.argv[1])
11. loaded_model.save_model('/tmp/a_model.json')
12. with open('/tmp/a_model.json', 'r') as fp:
13. jsonrepr = json.load(fp)
14. print(jsonrepr['learner']['gradient_booster']['model']['gbtree_model_param']['num_trees'])

We can run it as shown below (after saving the code snippet to a file xgb_tree_count.py):
python xgb_tree_count.py model-file-path

Making unsearchable pdf a searchable one

Try this command: $ ocrmypdf unsearchable.pdf this_will_be_searchable.pdf Here is the link for this interesting tool https://github.com/ocrmypdf/OCRmyPDF

Cleaning up unused container images to reclaim disk space

Below are the commands:

crictl -runtime-endpoint=unix:///run/containerd/containerd.sock rmi --prune -a

One more command for docker:

docker image prune -a

Dynamic programming to check interleaving strings

 Given strings A, B and C, this approach finds whether C is formed by the interleaving of strings A and B.

Let us assume, A = "ab", B="cd" and C="acbd", then we can say that C is formed by interleaving of strings A and B.

But if  A = "ab", B="cd" and C="adbc", then we can say that C cannot be formed by interleaving of strings A and B. This is due to the fact that in C, the character 'd' has come before C.

if  A = "ab", B="cd" and C="abcdx", then also we can say that C cannot be formed by interleaving of strings A and B. This is due to the fact that in C has a character which is not in A or B.

Now, let us assume C is a 50 character string and A is a 20 character string and B is 30 character string. If C can be formed by interleaving of A and B, then any prefix of C can be formed by interleaving some prefix of A and some prefix of B.

Assume A(n), B(n), C(n) denotes the prefix of A with n characters, prefix of B with first n characters and prefix of C with first n characters. 

Assume C(20) can be formed by interleaving of some prefix of A and B. We know that C(20) can be formed by some combining characters of A(0),B(20) or A(1), B(19) or A(2),B(18),.................., A(18), B(2) or A(19), B(1) or A(20),B(0) etc. There can be 21 such combinations and characters interleaved from some of these combinations result in C(20).

Now let us check if C(21) can be formed by interleaving some prefixes of A or B. It will be possible if A(i),B(j) gives C(20)  (i.e. i + j == 20) and either A[i+1] is same as the 21st character of C, or B[j+1] is the 21st character of C. Assume A[i+1] is same as  21st character of C, then we can say that A(i+1),B(j) can be interleaved to form C(21). 

In dynamic programming, we use the stored results previously computed. For checking C(21), we check for all combinations of A(i),B(j) where i + j = 20 and 0 <= i,j <= 20 and all combinations are already computed. 

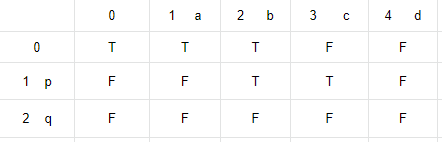
Now let us look at the below example. We will see how we check if C="abpcqd" is interleaving of A="abcd" and B="pq".

We initialize a two dimensional matrix of M size (2+1)x(4+1) and set all the cells to false. If M[i][j] is true, then first 'i' chars of B and first 'j' chars from A can be interleaved to get the string with first 'i + j' chars from C.

We have taken a matrix of 3x5 dimension.  Row 0 finds how much of C can be formed by interleaving only chars from A, and taking 0 chars from B.  M[0][0] = T (true) as null string from C can be formed by taking 0 chars from A and B.  

Now let us fill all the values for Row.  Row[0][1] = T, because  C(1) can be formed by A(1) alone.

Row[0][2] will be T again, as C(2) can be formed by A(2) alone. Row[0][3], Row[0,4] remain F as C(3) and hence C(4) also cannot be formed from A(3) and A(4) alone. 

Row[1][0] will remain false as C(1) cannot be formed from B(1) alone. Similarly Row[2][0] remains false.

  

Now let us start modifying Row[1] values. M[1][1] will remain F. Because though M[0][1] is T, C[1+1 - 0] = C[1] != B[0].  Row[1][2] will be T, as M[0][2] is true (that means C(3) is containing 'ab') and C[1+2 - 1]=C[2]==B[1].  Row[1][2] = T means, C(3) can be formed by interleaving B(1) and A(2). Now Row[1] is only for taking 1 char B[0] from B. As Row[1][2] is T, so for subsequent comparison on this row, we will use chars from A only. Row[1][3] will be T as Row[1][2] is T and C[3] == A[2]. Row[1][4] will remain F, as though Row[1][3] = True,  but C[4]!=A[3]

Similarly, we check Row[2]. Row[2][3] will be T as Row[1][3] == T and C[4] == B[2]. 

Row[2,4] will be T as Row[2][3] == T and C[5] == A[3].

Python implementation of above algorithm is given below:

'''
Given A, B, C, find whether C is formed by the interleaving of A and B.

Example:
1:
  A = "ab"
  B = "cd"
  C = "acdb"
  Here, C can be formed by the interleaving of A and B

2:
  A = "ab"
  B = "cd"
  C = "adbc"
  Here, C cannot be formed by the interleaving of A and B
  as 'd' and 'c' are coming out of orders in C.

2:
  A = "ab"
  B = "cd"
  C = "acd"
  Here, C cannot be formed by the interleaving of A and B
  as 'b' is missing in C

'''

def is_interleaving(first, second, interleaved):
    if len(first) + len(second) != len(interleaved):
        return False;
    if len(first) == 0:
        return second == interleaved
    if len(second) == 0:
        return first == interleaved

    # interleaved must start with 0th char of first or second string
    if not first[0] == interleaved[0]  and not second[0] == interleaved[0]:
        return False


    i = len(first) + 1
    j = len(second) + 1

    k = 0
    matrix = []
    while k < j:
        matrix.append([False] * i)
        k += 1

    # 0 char from first, 0 char from second is equal 0
    # char from interleaved
    matrix[0][0] = True


    # Now check how much of interleaved string can be formed 
    # by using 0 char from second and all others from first

    k = 1
    while k < i:
        if matrix[0][k - 1] and  (first[k - 1] == interleaved[k - 1]):
            matrix[0][k] = True
        else:
            break
        k += 1
    
    # Now check how much of interleaved string can be formed 
    # by using 0 char from first and all others from second

    k = 1
    while k < j:
        if matrix[0][0] and  (second[k - 1] == interleaved[k - 1]):
            matrix[k][0] = True
        else:
            break
        k += 1

    # Now we successively find out if interleaved[:n+m] can be formed
    # by interleaving first n chars from first and m chars from second
    # m varies from 1 to len(first)
    # n varies from 1 to len(second)
    # When we are on xth row of the matrix, we are actually trying to
    # check if (x - 1) chars from second string have been already seen,
    # and for that to happen, x - 2 chars have to be already present
    # in some prefix of interleaved. 

    k = 1
    ksecond_matched = False
    while k < j:
        #checking for a prefix of interleaved which can be formed
        #with k chars from second 
        l = 1
        ksecond_matched = matrix[k][0]
        while l < i:
            if not ksecond_matched:
                if matrix[k-1][l] and interleaved[k + l - 1] == second[k-1]:
                    matrix[k][l] = True
                    ksecond_matched = True
            else:
                # we have already matched k chars from second, check if a prefix
                # of length k + x can be obtained which is interleaved with
                # first k and x chars from second and first respectively
                if matrix[k][l - 1] and interleaved[k + l - 1] == first[l-1]:
                    matrix[k][l] = True
            l += 1
        k += 1
    
    return matrix[j - 1][i - 1]



test_data = [['a', 'b', 'ab', True],
             ['ab', '', 'ab', True],
             ['abc', 'd', 'abcd', True],
             ['ab', 'cd', 'abcd', True],
             ['ab', 'cd', 'abcde', False],
             ['ab', 'cde', 'aced', False],
             ['ab', 'cde', 'abcd' , False],
             ['ab', 'cde', 'aecdb', False],
             ['ab', 'cde', 'abcde', True]]


for row in test_data:
    if is_interleaving(row[0], row[1], row[2]) != row[3]:
        print '!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!Failed for ', row
    else:
        print 'Passed for', row

C++ implementation of above algorithm is given below:

#include <string>
#include <iostream>
#include <vector>
#include <algorithm>
#include <tuple>

using std::string;
using std::vector;
using std::cout;
using std::endl;
using std::tuple;
using std::make_tuple;
using std::get;


bool is_interleaving(const string& first, const string& second, 
    const string& interleaved)
{
    if (first.size() + second.size() != interleaved.size()) {
        return false;
    }
    if (first.size() == 0) {
        return second == interleaved;

    }
    if (second.size() == 0) {
        return first == interleaved;
    }
    
    if (second[0] != interleaved[0] && first[0] != interleaved[0]) {
        return false;
    }

    int i = first.size() + 1;
    int j = second.size() + 1;

    int k = 0;
    vector<vector<bool> > matrix;
    while (k++ < j) {
        matrix.push_back(vector<bool>(false,i));
    }

    // 0 char from first, 0 char from second is equal 0
    // char from interleaved
    matrix[0][0] = true;

    // Now check how much of interleaved string can be formed 
    // by using 0 char from second and all others from first

    k = 1;
    while (k < i) {
        if (matrix[0][k - 1] &&  (first[k - 1] == interleaved[k - 1]))
            matrix[0][k] = true;
        else
            break;
        k++;
    }
    
    // Now check how much of interleaved string can be formed 
    // by using 0 char from first and all others from second

    k = 1; 
    while (k < j) {
        if (matrix[0][0] &&  (second[k - 1] == interleaved[k - 1]))
            matrix[k][0] = true;
        else
            break;
        k++;
    }

    // Now we successively find out if interleaved[:n+m] can be formed
    // by interleaving first n chars from first and m chars from second
    // m varies from 1 to len(first)
    // n varies from 1 to len(second)
    // When we are on xth row of the matrix, we are actually trying to
    // check if (x - 1) chars from second string have been already seen,
    // and for that to happen, x - 2 chars have to be already present
    // in some prefix of interleaved. 

    k = 1;
    int l = 0;
    bool ksecond_matched = false;
    while (k < j) {
        //checking for a prefix of interleaved which can be formed
        //with k chars from second 
        l = 1;
        ksecond_matched = matrix[k][0];
        while (l < i) {
            if (!ksecond_matched) {
                if (matrix[k-1][l] && interleaved[k + l - 1] == second[k-1]) {
                    matrix[k][l] = true;
                    ksecond_matched = true;
                }
            } else {  
                // we have already matched k chars from second, check if a prefix
                // of length k + x can be obtained which is interleaved with
                // first k and x chars from second and first respectively
                if (matrix[k][l - 1] && interleaved[k + l - 1] == first[l-1])
                    matrix[k][l] = true;
            }
            l++;
        }
        k++;
    }
    return matrix[j - 1][i - 1];

}


// test run

int main() {
    cout << "Running some tests for the implementation" << endl;
    vector<tuple<string, string, string, bool> > inputs;
    inputs.push_back(make_tuple("a", "b", "ab", true));
    inputs.push_back(make_tuple("ab", "", "ab", true));
    inputs.push_back(make_tuple("abc", "d", "abcd", true));
    inputs.push_back(make_tuple("abc", "d", "acbd", false));
    inputs.push_back(make_tuple("a", "bc", "ab", false));
    inputs.push_back(make_tuple("ab", "bc", "abbc", true));
    inputs.push_back(make_tuple("ab", "bc", "acbb", false));
    inputs.push_back(make_tuple("ac", "bc", "abbc", false));

    for_each(inputs.begin(), inputs.end(), [](tuple<string, string, string, bool>& data) {
            cout << "Cheking for str1 = " << get<0>(data) << "  str2 = " << get<1>(data) 
                << "    interleaved = " << get<2>(data) 
                << "  expected=" << std::boolalpha << get<3>(data); 
            if (is_interleaving(get<0>(data), get<1>(data), get<2>(data)) != get<3>(data)){
                cout << " --> Failed " << endl;
            } else {
                cout << " --> Success " << endl;
            }
    });    
}

Extending Redis with new operations to expire data

Recently, one of my juniors was working on something which needed a distributed cache for sharing states across multiple process and saving states across restarts. Also, we needed the support for setting an expiry as we wanted to get the keys deleted on its own. We started with using MULTI command of Redis along with multiple SET command with expiry values. It turned out that, every command is sent to Redis separately for MULTI transactions and that was not a good choice for us. Also MSET command only allows to set values for the keys and not allow to set the expiry for the keys. So, MSET also we could not use.

We switched to Redis pipelining and that looks fine. But one small problem I noticed was that, for a pipleline with batch of 1000 SET operations, I get a response buffer containing the replies for all the 1000 operations. That was not a very good option for me. I wanted to have just one overall response just like we get in case of MSET or MSETNX commands.

I looked around and found that Redis server side scripting with Lua is a great option here and it can pretty much do the needful. Below code sample for doing the work:

local keycount = #KEYS
local argvcount = #ARGV
if ((keycount * 2) ~= argvcount )
then
    return 0
else
    local valstart  = 1
    for i = 1, #KEYS do
        redis.call('set', KEYS[i], ARGV[valstart], 'ex', ARGV[valstart + 1])
        valstart = valstart + 2
    end
    return 1
end

The code will take and execute a series of "set key value ex expiry_in_second" command internally and will return 1 on SUCCESS and 0 on failure.

We will use the redis EVALSHA command to create a custom command on Redis. I put the code snippet in a file named redis_call.lua and used SCRIPT LOAD command to load the script to Redis:

$ redis-cli -h localhost -p 6379  script load "$(cat redis_call.lua)"
"24d044a0dcc3af12f1b418d828083c475df48e8f"

So, I can use the SHA1 digest "24d044a0dcc3af12f1b418d828083c475df48e8f" to set value and expiry for multiple keys. Check the below output from redis-cli.

$ redis-cli -h localhost -p 6379
localhost:6379> EVALSHA 24d044a0dcc3af12f1b418d828083c475df48e8f 2  key1 key2 value1 1000 value2 20000
(integer) 1
localhost:6379> get key1 
"value1"
localhost:6379> get key2
"value2"
localhost:6379> ttl key1
(integer) 985
localhost:6379> ttl key2
(integer) 19981

So the script worked and here we got a custom command that simulates MSET with expiry for each key.

But still I felt that if we can get some built-in commands like MSETEX which is "MSET with expiry for each key" and MSETNXEX which is "MSETNX with expiry for each key", things would have been much better.
It is pretty simple in Redis to add a new command. So, I cloned Redis github repo, and added code for MSETEX and MSETNXEX. The help for the commands describe what they do:

$ redis-cli -h 127.0.0.1 -p 6379
127.0.0.1:6379> help msetex

  MSETEX [m/s] key value expiryseconds_or_milliseconds [key value expiryseconds_or_milliseconds]
  summary: Set multiple keys to multiple values with expiry set to seconds or millisconds. 
  since: 6.0.0
  group: string

127.0.0.1:6379> help msetnxex
  MSETNXEX [m/s] key value expiryseconds_or_milliseconds [key value expiryseconds_or_milliseconds]
  summary: Set multiple keys to multiple values with expiry set to seconds or millisconds, if none of the key exists
  since: 6.0.0
  group: string

127.0.0.1:6379> 

So, I can use MSETEX to SET values to multiple keys and also their expiry times. MSETNXEX only if none of the keys exists.  Below are some example of their uses:

127.0.0.1:6379> MSETEX m keya valuea 100000 keyb valueb 200000
OK
127.0.0.1:6379> MSETNXEX m keya valuea 10 keyc valueb 200000
(integer) 0
127.0.0.1:6379> MSETNXEX m keyd valued 9999 keyc valuec 20000
(integer) 1

My code for adding the 2 new commands can be accessed here . I have raised pull request. Hopefully, the PR will be accepted.

Creating a deployment on Azure using Terraform

In this post, I will explain how we may create a complete deployment on Azure using Terraform. How to do this using GCP and AWS will be covered in subsequent blogs.

Our deployment will have a Rest service with few APIs which are served by few Rest API servers sitting behind Nginx server(s). All the APIs are https and SSL termination happens at Nginx and internal traffic will be unencrypted.

Our services are microservice (a buzzword people love :)).
They are reliable.
They are highly available.
They are scalable.

As the services need to be highly available, we need to be running more than one instances of the service. So, we will have more than 1 instances of the services running. For this example, we will have just one service. As they have to scale out and in, so we need to dynamically create new instances of the service when there is high traffic or destroy few existing instnaces of the services when we detect usage is low. We can autoscale in and out at machine (virtual machine) level. But doing that at virtual machine level is not good for microservices. We should scale at light-weight service or microservice level. We will use Kubernetes for doing that staff for us. Kubernetes is a container-orchestration framework that fits well for microservices land. I really don't want to use Kubernetes to control my data stores as that doesn't buy me much. In this example, we will not be using Azure service for provisioning Kubernetes cluster, but we will provision that on our own. We don't want vendor lockin as far as possible :)

Please get the client_id, client_secret, tenant_id and subscription id from Azure console which will be internally used by packer to communicate with Azure via APIs.
Now let us create the VMs for Kubernetes on Azure using packer.  Below is the packer deifinition JSON (let us save it in file k8smachine.json)

{
  "builders": [{
    "type": "azure-arm",
    "subscription_id": "PUT YOUR SUBSCRIPTION_ID HERE",
    "client_id":        "PUT YOUR CLIENT_ID HERE",
    "client_secret":   "PUT YOUR CLIENT_SECRET HERE",
    "tenant_id":     "PUT YOUR TENANT_ID HERE",
    "managed_image_resource_group_name": "Nipun1",
    "managed_image_name": "Kubernetes_image",

    "os_type": "Linux",
    "image_publisher": "Canonical",
    "image_offer": "UbuntuServer",
    "image_sku": "18.04-LTS",

    "azure_tags": {
        "purpose": "kubernetes",
        "role": "compute"
    },

    "location": "East US",
    "vm_size": "Standard_DS2_v2"
  }],
  "provisioners": [{
    "execute_command": "chmod +x {{ .Path }}; {{ .Vars }} sudo -E sh '{{ .Path }}'",
    "inline": [
      "sudo apt-get install -qy docker.io",
      "sudo apt-get install -y apt-transport-https",
      "curl -s https://packages.cloud.google.com/apt/doc/apt-key.gpg | apt-key add -",
      "echo \"deb https://apt.kubernetes.io/ kubernetes-xenial main\" > /etc/apt/sources.list.d/kubernetes.list",
      "apt-get update",
      "apt-get install -y kubelet kubeadm kubectl",
      "apt-mark hold kubelet kubeadm kubectl",
      "wget https://github.com/coreos/flannel/releases/download/v0.11.0/flannel-v0.11.0-linux-amd64.tar.gz -P /home/ubuntu/"
    ],
    "inline_shebang": "/bin/sh -x",
    "type": "shell"
  }]
}

Here I am using "Nipun1" resource group which I have already created on Azure on location East US. You may have choose better names. The Azure VM image generated will have the name "Kuernetes_image"

Now we run the below command:

$ packer build k8smachine.json

And Ubuntu VM image with preinstalled Kubernetes binaries will be ready.

Now let us create the VM image with Elasticsearch binary and JRE (From OpenJDK) installed in it. Below is the packer JSON (let us put this in a file elasticsearch_vm_image.json).

{
  "builders": [{
    "type": "azure-arm",
    "subscription_id": "PUT YOUR SUBSCRIPTION_ID HERE",
    "client_id":        "PUT YOUR CLIENT_ID HERE",
    "client_secret":   "PUT YOUR CLIENT_SECRET HERE",
    "tenant_id":     "PUT YOUR TENANT_ID HERE",
    "managed_image_resource_group_name": "Nipun1",
    "managed_image_name": "elasticsearch_image",

    "os_type": "Linux",
    "image_publisher": "Canonical",
    "image_offer": "UbuntuServer",
    "image_sku": "18.04-LTS",

    "azure_tags": {
        "purpose": "elasticsearch",
        "role": "elasticsearchall"
    },

    "location": "East US",
    "vm_size": "Standard_DS2_v2"
  }],
  "provisioners": [{
    "execute_command": "chmod +x {{ .Path }}; {{ .Vars }} sudo -E sh '{{ .Path }}'",
    "inline": [
      "wget https://artifacts.elastic.co/downloads/elasticsearch/elasticsearch-5.6.9.deb",
      "apt-get -qy install openjdk-8-jre",
      "dpkg -i elasticsearch-5.6.9.deb",
      "rm elasticsearch-5.6.9.deb",
      "systemctl stop elasticsearch",
      "systemctl disable elasticsearch",
      "rm -rf /var/lib/elasticsearch/*",
      "rm -rf /var/log/elasticsearch/*"
    ],
    "inline_shebang": "/bin/bash -x",
    "type": "shell"
  }]
}

Now we create the Elasticsearch VM image by issuing the below command:

$ packer build  elasticsearch_vm_image.json

Let us create an Elasticsearch cluster now. We will use the terraform module for Elasticsearch from here.

Let us create the below terrform files:
main.tf

module createescluster {
    source = "github.com/nipuntalukdar/azureterraform/modules/escluster"
    azure_tenant_id = "${var.tenant_id}"
    azure_subscription_id = "${var.subscription_id}"
    azure_client_id = "${var.client_id}"
    azure_client_secret = "${var.client_secret}"
    ssh_public_key_path = "${var.ssh_pub_key}"
}

variables.tf

variable "subscription_id"  {
    description = "Azure subscription id"
    type = "string"

}
variable "client_id"  {
    description = "Azure client id"
    type = "string"
}
variable "client_secret"  {
    description = "Azure client secret"
    type = "string"
}
variable "tenant_id"  {
    description = "Azure tennant id"
    type = "string"
}
variable "ssh_pub_key"  {
    description = "SSH public key file"
    type = "string"

}

Put the above files main.tf and variables.tf in some directory and cd to that directory and issue the below commands:

$ terraform init

$ terraform apply

This will create a Elasticsearch cluster with 3 nodes in Azure.
If you want to destroy the Elasticsearch cluster, issue the below command:

$terraform destroy

Spark job concurrency and Understanding number of cores assigned to Jobs

Executors of Spark jobs are assigned certain number of cores. What do those number of cores actually mean? Do they actually tell that when an executor is running with 2 cores then the executor must be running in such a way that it uses only 2 cores of the machine, even when the machine has 16 CPU cores?
Actually things are somewhat different. Let me explain.
When we submit a job to Spark cluster, the driver communicates with master asking for resources to run. The number of cores is one such resource. Spark Master then makes a survey of the slaves or workers regarding the resource availability. It finds out the slave nodes with enough cores left and ask some of those worker(s) to run the job. The workers will create separate Java processes (executor processes) using our application jar and communicate with the driver to execute various stages of the job. Assume, there are one executor for a job which is using 2 cores, then that doesn't mean the executor java process will only use 2 cores of the machine it is running on. But it may use all the available cores of the machine. So, the "number of cores" is actually a parameter to assign the the slaves who are in a state to run the executors of a job.

Let us do some  exercise here. Let us start Spark master and slave where slave says that it has 2 cores to offer to execute jobs.

Now let us check what the Spark master UI is showing:

As we can see from the screenshot, there are 2 cores in the cluster and 0 of them are used right now. Those 2 are the ones advertised by lone worker running in the cluster.

Now let us run a small Spark streaming job. We will use Spark streaming with Kafka as the event source. I will not cover here how to setup Kafka and Zookeeper. We will setup a Kafka cluster and create a topic named "streaming". For this experiment we may create the topic with just one partition and no replication. The code for the simple streaming job is accessible here. 

We submit a Spark streaming job with application name "appa" and Kafka consumer group name "groupa" using the below command:

As you may see, the job is requesting for 2 cores (--executors-cores 2). After the job is started, let us visit the master URL again.

As we can see from the screenshot, there is one application running which has used 2 cores (i.e. all the available cores in the cluster). 

Now let us examine what are the actual CPU cores being used by the executor of the Spark job. (The machine has 4 CPUs).
First look at the process IDs of various java process.

Process 13667 is the Spark slave Java process, process 14936 is the executor Java process,  Process 13581 is the Spark master Java process and process 14860 is the driver Java process of our streaming job. We are interested to know how many cores executor (process 14936) is using at this moment. We execute "top" command (top -d 2 -p 14936 -H ) to get this information.

The last column in the above screenshot shows the last CPU core used by the thread. As we can see, the executor process is using all the 4 cores available. And, hence we can see for sure that "--executor-cores" parameter is just to identify which are the worker nodes that have enough resources to run the executors for a job. Once an executor process starts, the OS may schedule the threads of the executor process on all the CPU cores available on the machine.

As our Spark cluster now have "zero cores left" for executing new Job, so submitting new Job will only queue them and they won't make any progress until the first job is killed. 

A tool for Kafka consumers details

I was looking for a tool to set the offsets of Kafka high level consumers. After doing some search, I decided to built one of my own. The tool helps to get the consumer details of a consumer group, get the offsets of a consumer group and also set the offsets of the partitions consumed by a consumer group. Sometimes setting the consumer offsets at desired position is required to skip some messages, and also to re-process the messages from the same consumer group.

The tool is available here
The link also has the details about how to install and run the tool.
Hopefully, it may help somebody.


Below are some examples from running the tool:

$ kafka_consumer_tool --consumergroup newgroup --command commitoffsets --inputjson topic_offsets.json
2017/10/15 15:33:52 Commiting offsets
2017/10/15 15:33:52 Topic: a1, Partition: 6,  Offset committed successfully
2017/10/15 15:33:52 Topic: a1, Partition: 7,  Offset committed successfully
2017/10/15 15:33:52 Topic: a1, Partition: 8,  Offset committed successfully
2017/10/15 15:33:52 Topic: a1, Partition: 1,  Offset committed successfully
2017/10/15 15:33:52 Topic: a1, Partition: 3,  Offset committed successfully
2017/10/15 15:33:52 Topic: a1, Partition: 5,  Offset committed successfully
2017/10/15 15:33:52 Topic: a1, Partition: 2,  Offset committed successfully
2017/10/15 15:33:52 Topic: a1, Partition: 4,  Offset committed successfully
2017/10/15 15:33:52 Topic: a2, Partition: 1,  Offset committed successfully
2017/10/15 15:33:52 Topic: a2, Partition: 3,  Offset committed successfully
2017/10/15 15:33:52 Topic: a3, Partition: 1,  Offset committed successfully
2017/10/15 15:33:52 Topic: a3, Partition: 3,  Offset committed successfully

$ kafka_consumer_tool --consumergroup newgroup --command getoffsets --topics a1,a3
2017/10/15 15:35:48 Current offset details:
2017/10/15 15:35:48 Topic: a1, Partition: 0, Offset: 1830
2017/10/15 15:35:48 Topic: a1, Partition: 1, Offset: 20
2017/10/15 15:35:48 Topic: a1, Partition: 2, Offset: 1
2017/10/15 15:35:48 Topic: a1, Partition: 3, Offset: 0
2017/10/15 15:35:48 Topic: a1, Partition: 4, Offset: 1
2017/10/15 15:35:48 Topic: a1, Partition: 5, Offset: 1
2017/10/15 15:35:48 Topic: a1, Partition: 6, Offset: 1
2017/10/15 15:35:48 Topic: a1, Partition: 7, Offset: 100
2017/10/15 15:35:48 Topic: a1, Partition: 8, Offset: 1
2017/10/15 15:35:48 Topic: a1, Partition: 9, Offset: 1812
2017/10/15 15:35:48 Topic: a1, Partition: 10, Offset: 1920
2017/10/15 15:35:48 Topic: a1, Partition: 11, Offset: 1920
2017/10/15 15:35:48 Topic: a1, Partition: 12, Offset: 1908
2017/10/15 15:35:48 Topic: a1, Partition: 13, Offset: 1818
2017/10/15 15:35:48 Topic: a1, Partition: 14, Offset: 1908
2017/10/15 15:35:48 Topic: a1, Partition: 15, Offset: 1926
2017/10/15 15:35:48 Topic: a1, Partition: 16, Offset: 1860
2017/10/15 15:35:48 Topic: a1, Partition: 17, Offset: 1860
2017/10/15 15:35:48 Topic: a1, Partition: 18, Offset: 1830
2017/10/15 15:35:48 Topic: a1, Partition: 19, Offset: 1836
2017/10/15 15:35:48 Topic: a1, Partition: 20, Offset: 1866
2017/10/15 15:35:48 Topic: a1, Partition: 21, Offset: 1896
2017/10/15 15:35:48 Topic: a1, Partition: 22, Offset: 1902
2017/10/15 15:35:48 Topic: a1, Partition: 23, Offset: 1932
2017/10/15 15:35:48 Topic: a1, Partition: 24, Offset: 1956
2017/10/15 15:35:48 Topic: a1, Partition: 25, Offset: 1842
2017/10/15 15:35:48 Topic: a1, Partition: 26, Offset: 1890
2017/10/15 15:35:48 Topic: a1, Partition: 27, Offset: 1920
2017/10/15 15:35:48 Topic: a1, Partition: 28, Offset: 1848
2017/10/15 15:35:48 Topic: a1, Partition: 29, Offset: 1734
2017/10/15 15:35:48 Topic: a1, Partition: 30, Offset: 1746
2017/10/15 15:35:48 Topic: a1, Partition: 31, Offset: 1872
2017/10/15 15:35:48 Topic: a3, Partition: 0, Offset: 615
2017/10/15 15:35:48 Topic: a3, Partition: 1, Offset: 2
2017/10/15 15:35:48 Topic: a3, Partition: 2, Offset: 623
2017/10/15 15:35:48 Topic: a3, Partition: 3, Offset: 4
2017/10/15 15:35:48 Topic: a3, Partition: 4, Offset: 627
2017/10/15 15:35:48 Topic: a3, Partition: 5, Offset: 641
2017/10/15 15:35:48 Topic: a3, Partition: 6, Offset: 632
2017/10/15 15:35:48 Topic: a3, Partition: 7, Offset: 631
2017/10/15 15:35:48 Topic: a3, Partition: 8, Offset: 633
2017/10/15 15:35:48 Topic: a3, Partition: 9, Offset: 609
2017/10/15 15:35:48 Topic: a3, Partition: 10, Offset: 635
2017/10/15 15:35:48 Topic: a3, Partition: 11, Offset: 640
2017/10/15 15:35:48 Topic: a3, Partition: 12, Offset: 626
2017/10/15 15:35:48 Topic: a3, Partition: 13, Offset: 592
2017/10/15 15:35:48 Topic: a3, Partition: 14, Offset: 609
2017/10/15 15:35:48 Topic: a3, Partition: 15, Offset: 633


$ kafka_consumer_tool --consumergroup newgroup --command listconsumers
2017/10/15 15:36:47 Group: newgroup,  state: Stable
2017/10/15 15:36:47 id: myid5-45d71997-3ed2-4443-9f1b-30d972aefc35, host: /192.168.1.3, clientid: myid5
2017/10/15 15:36:47 id: myid1-0fa736ca-56a6-495d-9887-83f63396e4de, host: /192.168.1.3, clientid: myid1
2017/10/15 15:36:47 id: myid6-4ad5c512-6599-4706-802c-872b4257e5c8, host: /192.168.1.3, clientid: myid6
2017/10/15 15:36:47 id: myid7-b7a3c69b-32ad-43c7-ab87-467eee5d65d9, host: /192.168.1.3, clientid: myid7
2017/10/15 15:36:47 id: myid4-1c4f50a1-8bfd-4752-9371-0d0cd31407f6, host: /192.168.1.3, clientid: myid4
2017/10/15 15:36:47 id: myid2-581bbba8-003e-4322-adce-18573c71dac3, host: /192.168.1.3, clientid: myid2
2017/10/15 15:36:47 id: myid0-48bb6ae8-b6c2-4893-a34d-8f842ef2f61c, host: /192.168.1.3, clientid: myid0
2017/10/15 15:36:47 id: myid3-548e4d32-a458-4edd-b9da-084a07db0440, host: /192.168.1.3, clientid: myid3
2017/10/15 15:36:47 id: myid9-bacf18ad-9e5c-45ca-92e2-c5fa85ea9963, host: /192.168.1.3, clientid: myid9
2017/10/15 15:36:47 id: myid8-796f0609-9734-4d75-b35e-21efbbf7d6ee, host: /192.168.1.3, clientid: myid8
Nipun:kafka_consumer_tool samrat$